Michael Vitus

My core research is at the intersection of robotics, control and estimation theory, and optimization with an emphasis on enhancing real-time autonomy of robotic systems. In the past, I have worked on many different hardware platforms including a lunar rover, an aerobatic helicopter, and a quadrotor helicopter. Through my experiences, I have realized that theoretical research and hardware platforms as well as large scale applications should be and are intertwined.

You'll find a more detailed description of some of my research below.

STARMAC Quadrotor

The Stanford Testbed of Autonomous Rotorcraft for Multi-Agent Control (STARMAC) is a fleet of small, lightweight, low cost, unmanned aerial vehicles that we are using to demonstrate new concepts in multi agent control. Each vehicle can carry a variety of sensors, including a kinect sensor, laser range-finder, stereo/mono camera and avalanche rescue beacon sensor.

STARMAC was one of the first successful autonomous quadrotor platforms and has been used in a variety of experiments: search and rescue, decentralized collision avoidance, stochastic and deterministic motion planning, sensor placement, autonomous landing and robust controller synthesis.

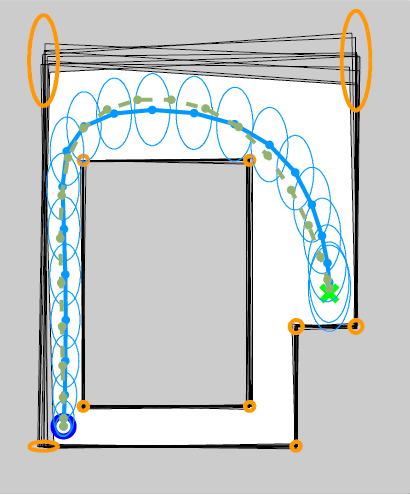
Most recently, we demonstrated successful aerobatic maneuvers with theoretical guarantees on safety. To successfully complete a backflip maneuver we analyzed the system to provide conditions on the quadrotor's state that ensured, even with disturbances, it could safely return to a stable hovering condition. This was accomplished by modeling the quadrotor in a hybrid dynamics framework for the design of guaranteed safe switching regions which were constructed using reachable sets calculated via a Hamilton-Jacobi differential game formulation. A video explanation is shown below on the right.

STARMAC Overview Video Backflip Explanation Video

Visit the STARMAC Webpage for more information.
Some news articles: Engadget Article on Backflip, PodTech, Engineering TV, Gizmo Watch, Funny Engadget article

Stochastic Motion Planning

With the advances in technology of robotic systems, there has been a growing number of robots deployed to perform challenging tasks such as: search and rescue, reconnaissance, surveillance, and disaster response. In all of these tasks, there is a pressing need for algorithms to plan safe trajectories through complex environments. In the planning process the system cannot be assumed to be deterministic, rather the inherit uncertainty of the system must be accounted for explicitly in order to maximize the success of the resulting plan.

The uncertainty in the planning problem arises from three different sources: (i) motion uncertainty, (ii) sensing noise and (iii) environment uncertainty. The presence of these uncertainties means that the exact system state is never truly known. Consequently, in order to maximize the probability of success, the planning problem must be performed in the space of probability distributions of the system, defined as the belief space. For a stochastic system, however, planning in the belief space is not enough to guarantee success because there is always a small probability that a large disturbance will be experienced. Therefore, a trade-off must be made between the conservativeness of the plan and the performance of the system.

This work formulates the stochastic path planning problem as a chance constrained optimization program. For known environments the optimization program is convex but for uncertain environments the program is not necessarily convex. To overcome the non-convexity, a novel hybrid method is proposed that uses both sampling and analytical functions to represent the uncertainty which results in a convex optimization under certain conditions. This dual representation drastically reduces the computational complexity, enabling real-time execution of these algorithms.

The stochastic motion planning algorithms were evaluated on a quadrotor unmanned aerial vehicle equipped with a Kinect sensor navigating through a 3D environment. A video of this demonstration is shown below. To our knowledge, this is the first successful, real-time experimental demonstration of chance constrained control through uncertain environments. All the algorithms were executed in real-time without any human intervention. In this example there are two sources of environment uncertainty: (i) the obstacle locations are not known exactly due to the sensing error of the Kinect sensor (which can vary from 2cm-10cm), (ii) some corridors have a probability of being blocked. Consequently, the quadrotor will have to solve the dual control problem of trading off between gaining new information to enable shorter paths or taking known obstacle-free paths.

In this demonstration, all the algorithms are being solved online, and the 3D map is being updated with the incoming data from the Kinect sensor. Note, the Kinect sensor has a hard time sensing black objects, which is why white poster board is placed over the cabinet door.

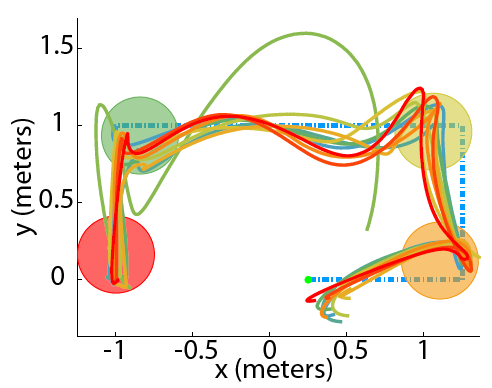
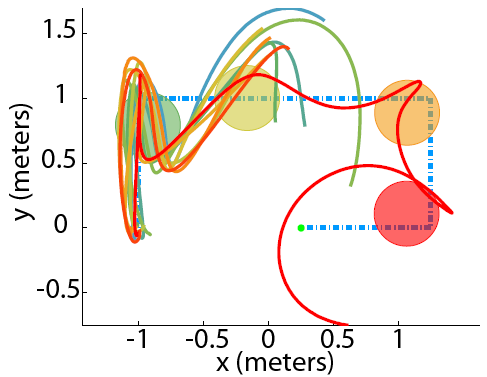
Motion Planning

Randomized methods, such as probabilistic roadmaps, have been proposed to solve the obstacle avoidance problem, particularly for instances with a very large number of constraints. However, the resulting paths are generally not optimized in distance or time, and can result in winding paths if the vehicle dynamics are incorporated. Formulations using mixed interger linear programming (MILP) have been proposed which provide the optimal solution, but suffer from scalability issues as the number of obstacles, and hence the number of integer variables, increases.

In order to address MILP scalability and provide near optimal solutions, a novel three-stage algorithm, Tunnel-MILP, is presented which first computes a desirable path through the environment without considering dynamics, then generates a sequence of convex polytopes containing the desired path, and finally poses a MILP to identify a suitable dynamically feasible path. Simulation results reveal a significant decrease in the required computation time.

Tunnel-MILP has been successfully demonstrated on the STARMAC platform.

Sensor Placement for Improved Robotic Navigation

The sensor deployment problem involves a set of fixed sensors used to estimate the vehicle state (e.g. position, orientation and velocity) while attempting to follow a pre-planned trajectory through the environment. Since the sensor can only provide a measurement to the vehicle when it is within range, the deployment of the sensors will have a major impact on the ability of the vehicle to follow the trajectory. The problem addressed here is to optimally place the sensors in the environment to maximize the probability of the vehicle successfully following the intended trajectory. To prevent an overconfident solution, the uncertainty of the vehicle's state is taken into account in determining whether it can receive a measurement from a sensor.

There are many motivating examples for this work. One example is the placement of sensors to minimize the uncertainty of a vehicle following a pre-planned trajectory. There are several applications for which a pre-planned trajectory exists and is repeatedly used including automated supply chains, autonomous construction and disaster site cleanup. In these applications, the proposed work can provide better performance with fewer sensors than existing solutions. Another potential application is tracking building occupants' behavior to enable energy efficient control.

The results of the experimental trials are depicted in plots on the left; the planning with and without uncertainty cases are shown on the top and bottom, respectively. The pre-planned trajectory is shown by the blue, dash-dotted line. Ten experimental trials were conducted for each sensor placement strategy. When accounting for uncertainty, nine out of the ten tests were successfully flown by the quadrotor vehicle. The test that failed required human intervention because the vehicle initially missed the second sensor's measurement region, causing the vehicle to oscillate around the trajectory. In contrast, the sensor placement strategy that didn't account for the uncertainty of the vehicle required human intervention for all ten trials to prevent a crash.

Planning without uncertainty Planning with uncertainty

STARMAC Overview Video	Backflip Explanation Video

Visit the STARMAC Webpage for more information. Some news articles: Engadget Article on Backflip, PodTech, Engineering TV, Gizmo Watch, Funny Engadget article

	Stochastic Motion Planning With the advances in technology of robotic systems, there has been a growing number of robots deployed to perform challenging tasks such as: search and rescue, reconnaissance, surveillance, and disaster response. In all of these tasks, there is a pressing need for algorithms to plan safe trajectories through complex environments. In the planning process the system cannot be assumed to be deterministic, rather the inherit uncertainty of the system must be accounted for explicitly in order to maximize the success of the resulting plan. The uncertainty in the planning problem arises from three different sources: (i) motion uncertainty, (ii) sensing noise and (iii) environment uncertainty. The presence of these uncertainties means that the exact system state is never truly known. Consequently, in order to maximize the probability of success, the planning problem must be performed in the space of probability distributions of the system, defined as the belief space. For a stochastic system, however, planning in the belief space is not enough to guarantee success because there is always a small probability that a large disturbance will be experienced. Therefore, a trade-off must be made between the conservativeness of the plan and the performance of the system. This work formulates the stochastic path planning problem as a chance constrained optimization program. For known environments the optimization program is convex but for uncertain environments the program is not necessarily convex. To overcome the non-convexity, a novel hybrid method is proposed that uses both sampling and analytical functions to represent the uncertainty which results in a convex optimization under certain conditions. This dual representation drastically reduces the computational complexity, enabling real-time execution of these algorithms. The stochastic motion planning algorithms were evaluated on a quadrotor unmanned aerial vehicle equipped with a Kinect sensor navigating through a 3D environment. A video of this demonstration is shown below. To our knowledge, this is the first successful, real-time experimental demonstration of chance constrained control through uncertain environments. All the algorithms were executed in real-time without any human intervention. In this example there are two sources of environment uncertainty: (i) the obstacle locations are not known exactly due to the sensing error of the Kinect sensor (which can vary from 2cm-10cm), (ii) some corridors have a probability of being blocked. Consequently, the quadrotor will have to solve the dual control problem of trading off between gaining new information to enable shorter paths or taking known obstacle-free paths. In this demonstration, all the algorithms are being solved online, and the 3D map is being updated with the incoming data from the Kinect sensor. Note, the Kinect sensor has a hard time sensing black objects, which is why white poster board is placed over the cabinet door.

Motion Planning Randomized methods, such as probabilistic roadmaps, have been proposed to solve the obstacle avoidance problem, particularly for instances with a very large number of constraints. However, the resulting paths are generally not optimized in distance or time, and can result in winding paths if the vehicle dynamics are incorporated. Formulations using mixed interger linear programming (MILP) have been proposed which provide the optimal solution, but suffer from scalability issues as the number of obstacles, and hence the number of integer variables, increases. In order to address MILP scalability and provide near optimal solutions, a novel three-stage algorithm, Tunnel-MILP, is presented which first computes a desirable path through the environment without considering dynamics, then generates a sequence of convex polytopes containing the desired path, and finally poses a MILP to identify a suitable dynamically feasible path. Simulation results reveal a significant decrease in the required computation time. Tunnel-MILP has been successfully demonstrated on the STARMAC platform.

The approximate locations of the sensors are overlayed as blue ellipses in the videos.

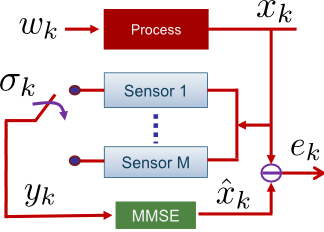
Optimal Scheduling of Kalman Filters

The sensor scheduling problem consists of selecting a subset of the available sensors to estimate the system state while reducing the estimation cost (e.g. energy consumption and communication overheads). Many motivating applications can benefit from this technology, for example: (a) tracking building occupants to enable energy efficient control for adjusting power settings, (b) interference between sensors such as with sonar sensors used in terrain relative navigation, (c) path planning for active sensing in uncertain environments.

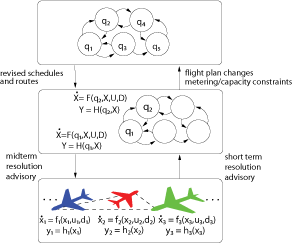
Previous methods were based on heuristic approaches, such as greedy or convex relaxations, which provide no performance guarantees even for linear, Gaussian systems. Our approach leverages properties of the Ricatti recursion to establish convex conditions to eliminate branches from the search tree resulting in no more error than a given threshold. (with the resulting less than a given threshold) These properties can be utilized to develop an efficient, tractable algorithm to solve complex systems.

Collision Avoidance Algorithms for Aircraft

The goal of the Next Generation Air Transportation System (NGATS) is to increase the capacity of the National AirSpace (NAS) while increasing the efficiency and safety of the airspace. Currently, there are many collision avoidance algorithms that exist or are being developed for different time scales. Even though each individual algorithm may provide safety between the aircraft, when combined to form a hybrid collision avoidance system for all time scales, safety cannot be guaranteed. Therefore to facilitate NGATS, methods need to be developed for analyzing the interaction between airborne collision avoidance systems and tactical separation assurance tools in Air Traffic Control (ATC). Furthermore, procedures need to be designed to guarantee that these collision avoidance and separation assurance tools do not conflict with each other, but rather operate together safely and efficiently. This interoperability of collision avoidance functions is integral to the design of NGATS.

Dark Navigation

This project is part of CMU's Lunar Rover Initiative. It is developing Scarab to evaluate and demonstrate a combined drilling and science rover platform for lunar exploration. One of the major goals of the rover is to explore dark and permanently shadowed zones, such as the interior of polar craters on the Moon. For a robotic explorer to operate in these areas, the robot must be capable of navigating in unstructured, natural terrain with little (or no) ambient illumination. This requires appropriate sensing to determine the robot's position, to detect obstacles/hazards, and to safely control autonomous motions. My work designed, developed, and implemented terrain analysis techniques for planar laser scanners. The algorithms were successfully tested on over 500m of autonomous driving.

Visit the Scarab Webpage for more information.
Some news articles: Engadget, Robot Trends, Post Gazette, Universe Today

GPS Positioning System for an Aerobatic Helicopter

When a helicopter is under autonomous control, it obtains information from a suite of instruments, which typically include a single GPS receiver. GPS has to maintain a line-of-sight to at least 4 satellites to provide a reliable estimate of the helicopter's position. If the helicopter is performing aggressive aerobatic maneuvers, the single GPS receiver is constantly losing line-of-sight to the satellites, and therefore it will not be able provide a reliable estimate of the helicopter's position.

The goal of the project was to develop a method of maintaining a reliable estimate of the position of the helicopter while it is performing aggressive aerobatic maneuvers such as rolls. The method that was formulated used multiple GPS receivers positioned precisely around the helicopter. Since the inertial measurement unit (IMU) of the helicopter is great for providing estimates of the roll, pitch, and yaw angles, the relative positioning of the multiple GPS receivers to each other is known. After the initial integer ambiguity is solved and the helicopter performs aggressive maneuvers, the position estimate from one GPS receiver can be passed to the other receivers to solve for their new integer ambiguities. Also, if a single GPS receiver doesn't have enough satellites to solve for a position estimate of its own, it can be coupled with the other GPS receivers so that all the satellites that are in view will be used for a more accurate position estimate. Although in theory the passing of the position estimate from one receiver to another works, the actual hardware had a large delay in obtaining the phase lock after being obstructed for a short time. Therefore, when the helicopter would roll the receivers wouldn't be able to obtain phase lock before they were obstructed again.